Time Complexity of Recursive Fibonacci

The algorithm (given in C) for the n^th fibonacci number is this:

int fibonacci(int n) {
  if (n == 1 || n == 2) return 1;
  return fibonacci(n - 1) + fibonacci(n - 2);
}

It's simple enough, but the runtime complexity isn't entirely obvious. An initial assumption might be that it is O(2ⁿ), as it is a recursive formula that branches twice each call, but this isn't the best upper-bound.

The reason for this is that the branch of the recursive call calculating fibonacci(n - 2) will terminate faster than the one calculating fibonacci(n - 1), this fact being compounded on each call, so there's one path that will get to a base case in n / 2 calls, and another getting there in n calls, with all sorts of other paths in between.

The key to getting the proper complexity of fibonacci, then, is to count how many times base cases are reached, as we know that if there are, say, n base cases reached, then there couldn't be more than 2n total functions calls*, and O(2n) = O(n).

Finding the number of base cases reached is actually quite easy; it's fibonacci(n). This can be verified easily enough with the following C program, which takes a number n and returns whether the n^th fibonacci number is equal to the number of bases cases reached in its calculation.

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

int fibonacci(int num, int *count);
bool fib_base_cases(int n);

int main() {
  int num;
  printf("Enter Number: ");
  scanf("%d", &num);

  printf("%s\n", fib_base_cases(num) ? "true" : "false");

  return 0;
}

bool fib_base_cases(int n) {
  int result = 0;
  int fib = fibonacci(n, &result);
  return result == fib;
}

int fibonacci(int num, int *count) {
  if (num == 1 || num == 2) {
    (*count)++;
    return 1;
  }

  return fibonacci(num - 1, count) + fibonacci(num - 2, count);
}

But given that this program will take an extraordinary amount of time even for small inputs, a short informal proof is preferable:

Given that the base case returns 1, and fibonacci(n) is equal to the sum of all base cases (convince yourself of this), fibonacci(n) must equal the number of base cases reached.

Thus, if we find an explicit formula for the n^th fibonacci number, we can find the complexity of fibonacci.

Fortunately, an explicit formula has already been derived, courtesy of the brilliant French-British mathematician Abraham de Moivre. He discovered, among many other things, that

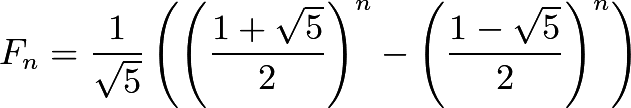
Where F_n is the n^th fibonacci number.

The first term in Binet's Formula is also known as the golden ratio, typically denoted with the Greek letter ϕ.

Thus, the complexity of fibonacci is O(F_n) = O(ϕⁿ). This is approximately O(1.618ⁿ). Still awful, but a little better than the initial assumption of O(2ⁿ).